Basics
Operators and Data Type
Bitwise Operators in C/C++
AND (&), OR (|), NOT (~), XOR (^), LEFT SHIFT (<<), RIGHT SHIFT (>>)
The left shift and right shift operators should not be used for negative numbers. If any of the operands is a negative number, it results in undefined behaviour. For example results of both -1 << 1 and 1 << -1 is undefined.
Also, if the number is shifted more than the size of integer, the behaviour is undefined. For example, 1 << 33 is undefined if integers are stored using 32 bits. See this for more details.
int Data Type
In C/C++ int variable is 32-bits in size and can contain any integer between −231 and 231 − 1.
The first bit in a signed representation is the sign of the number (0 for non-negative numbers and 1 for negative numbers), and the remaining n − 1 bits contain the magnitude of the number. Two’s complement is used to represent negative numbers.
Properties
AND (&) - Used to “mask” bits, it can check for set bits and we can mask a number using another.
OR (|) - Used to set bits.
NOT (~) - 1’s complement of a number.
XOR (^) - Exclusivity between two numbers' bits. Toggling bits.
LEFT SHIFT (<<) - Left shift performed k times multiplies the number by 2k
RIGHT SHIFT (<<) - Right shift performed k times divides the number by 2k
2’s Complement of n = -n
Binary Negative - 2s Complement Form
We needed a system to represent negative numbers in binary. 1s complement won’t work because it will yield two representations for 0, 0000 (+0) and its 1s complement 1111 (-0 wtf lol).
Finally we settled on 2s complement to represent negative numbers, this way zero has a single representation.
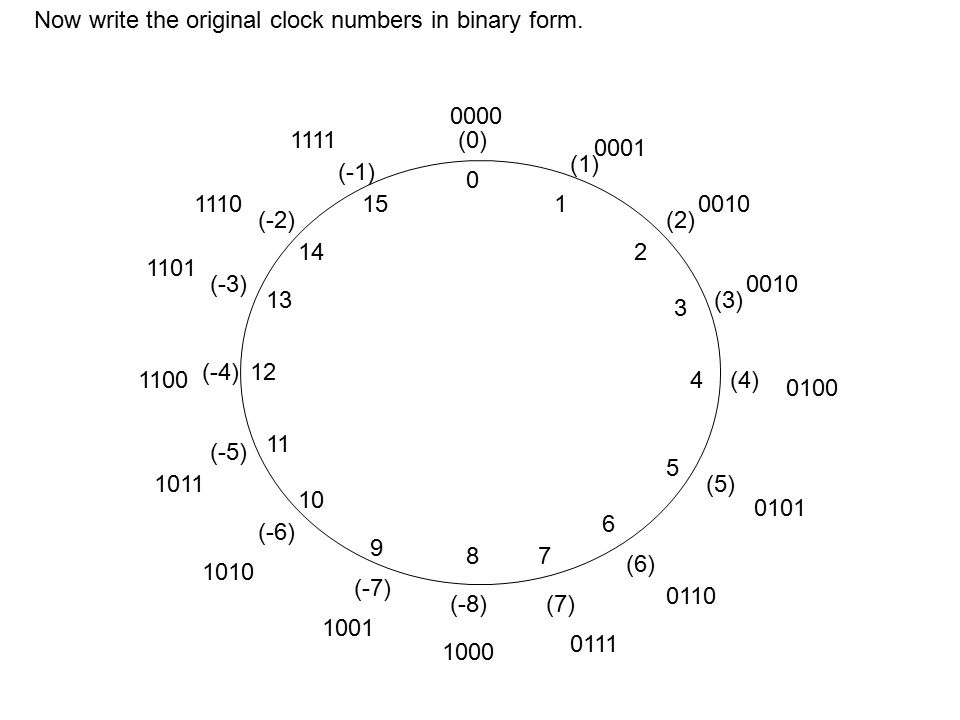
With n bits, we can represent numbers in the range [−2n/2, 2n/2 − 1] which is often written as [−2n-1, 2n-1 − 1].
After 2n-1 - 1 positives, numbers loop around to lowest negative value as shown in the below diagram:
// loop around demonstration with int overflow in C++
#include <iostream>
#include <climits>
int main() {
std::cout << INT_MAX + 1; // overflow; prints "-2147483648" (lowest negative)
return 0;
}
It is not always possible to see a negative number written in binary form and tell what number it is by magnitude calc using powers of 2. It works for -4 = 1100, +4 = 0100 but not for -5 = 1011, +5 = 0101 and many others. Hence, ssomeone needs to explicitly tell us that it is a 2s complement binary numbers.
since, 2s complement = 1s complement + 1
-n = ~n + 1
=> ~n = -(n+1)
Sign Bit
Often the MSB is said to be “sign bit” in programming languages. It is not explicitly decided (changed) but is the feature of using 2s complement signed binary number system.
00001 = +1
11111 = -1
We can judge the sign of a binary number by seeing only its MSB (that's why its caled a Sign Bit)
Addition (+)
Addition is not really native to binary numbers. We often end up with overflown carry bit, the reason why adder circuits like half & full have two outputs, a carry and a sum.
In programming languages, apart from 0, addition of numbers with their negatives in 2c complement system has overflow which is discarded to get result as 0.